[ad3]
La mia analisi riguarda il funzionamento di un Rock Shox Monarch Plus Debonair ed i dati sono relativi ad esso, ma i concetti alla base dei calcoli ed i risultati (NON numerici ovviamente) sono validi per qualsiasi ammortizzatore ad aria dotato di sistema a valvola singola.
In questa prima analisi non terrò conto dell’influenza dell’idraulica, quindi l’analisi delle compressioni è da ritenersi valida in regime statico e non in regime dinamico.
Misurazione empirica
Sono partito con l’acquisire empiricamente alcuni dati di riferimento e di controllo (che come vedremo sono stati successivamente controprovati dalla teoria) grazie ai miei potenti mezzi, ovvero un bilancia per pesarmi, una pompetta per sospensioni con manometro e la mia bellissima Specialized Enduro 650b con Rock Shox Monarch Plus Debonair nuovo fiammante.

I dati rilevati in partenza sono i seguenti:
Ammortizzatore senza spessori nelle camere.
Peso rider vestito 82 kg
SAG voluto 30%
Pressione necessaria rilevata 200 Psi.
Successivamente ho aperto l’ammortizzatore ed ho rilevato empiricamente con dell’acqua e un paio di pipette i volumi delle camere interne destinati ad ospitare l’aria.
Poi finalmente mi sono lanciato nei calcoli teorici che a me piacciono tanto.
Ammortizzatore ad aria a valvola singola
Spieghiamo innanzitutto come è fatto un ammortizzatore ad aria a valvola singola a volume variabile:
(n.b.: le misure del disegno non corrispondono alla realtà ma sono state modificate per renderlo più comprensibile. Le camere 2 e 4 ad esempio sono molto più ridotte)
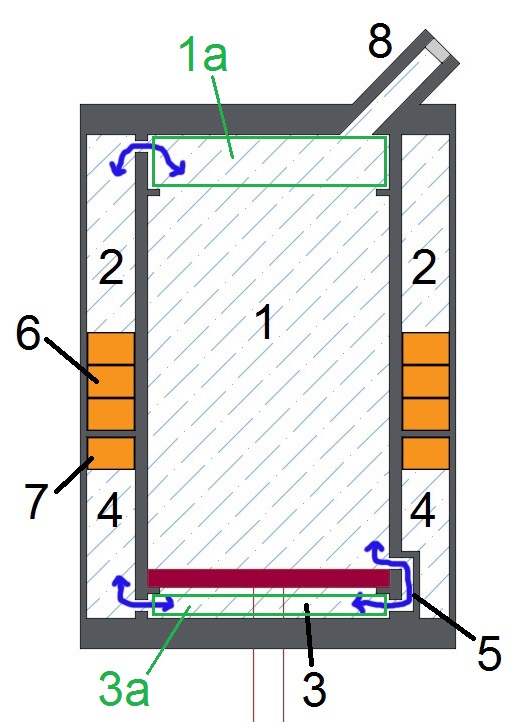

Il disegno in FIG. 1 rappresenta l’ammortizzatore (schematizzato) in sezione longitudinale. Esso è composto da due cilindri concentrici.
All’interno del cilindro interno scorre il pistone a tenuta, il quale separa il volume in due camere principali: camera positiva (1) superiormente e camera negativa (3) inferiormente.
Le due camere principali sono in costante comunicazione, attraverso due fori, con la rispettiva camera spessorabile (2) e (4), la cui utilità è ovviamente quella di poter ospitare gli spessori (6) e (7) per la modifica dei volumi.
Camera positiva e camera negativa sono in comunicazione solamente ad ammortizzatore completamente esteso, in questa situazione il passaggio tra le due camere (5) viene aperto e vi è un equilibrio di pressione tra le due camere.
L’aria all’interno dell’ammortizzatore viene introdotta dalla valvola (8) in comunicazione con la camera positiva, ed essendo tale operazione da farsi rigorosamente a bici scarica l’aria può defluire anche in camera negativa.
La corsa del pistone è delimitata dai dentini superiori (ammo a pacco) e dai dentini inferiori (ammo scarico come in FIG. 1 e FIG. 3) ed è ovviamente pari alla corsa dell’ammortizzatore stesso.
I due volumi nelle camere principali che non sono accessibili al pistone (1a, 3a) li chiamerò volume di compensazione per la camera positiva (1a) e volume di compensazione per la camera negativa (3a), il loro scopo è quello di evitare che con ammo completamente spessorato le pressioni tendano a + infinito.
Il numero massimo di spessori consentiti sarà tale da non ostruire i passaggi tra le due camere principali e le relative camere spessorabili, per il Monarch Plus Debonair tale numero di spessori è 9 per la camera positiva e 5 per quella negativa.
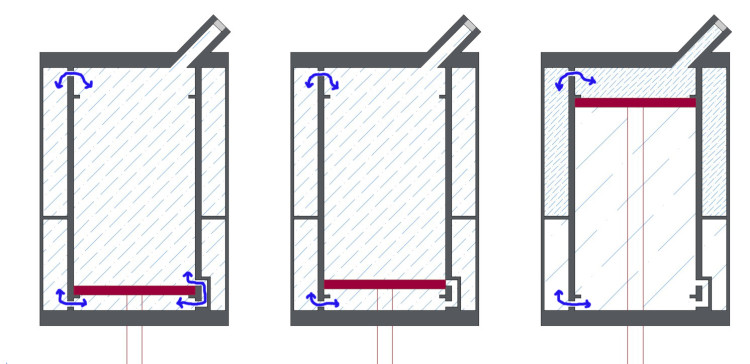
In FIG. 4 è rappresentato l’ ammortizzatore a riposo, quindi con stelo completamente esteso. In questa situazione la valvola di comunicazione tra camera positiva e negativa risulta aperta, quindi gonfiando l’ammortizzatore attraverso la valvola, la pressione si equilibrerà nelle due camere.
In FIG. 5 vediamo come l’ammortizzatore soggetto alla minima compressione farà si che il pistone andrà a chiudere la valvola di comunicazione. Da questo momento in poi le due camere sono separate.
In FIG. 6 vediamo l’ammortizzatore alla massima compressione (a pacco), il volume in camera positiva principale sarà pari al volume di compensazione per la camera positiva (FIG. 1 – 1a). Da notare come all’alzarsi del pistone (ammo che si comprime) la pressione in camera positiva andrà aumentando (tratteggio più fitto), mentre la pressione in camera negativa andrà diminuendo (tratteggio più rado).
Introduzione analisi grafica
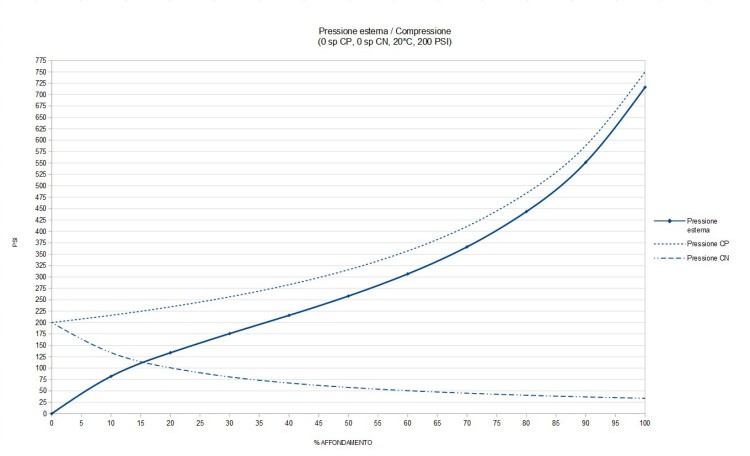
Nel grafico di FIG. 7, frutto dei miei sudatissimi calcoli, è rappresentato con le linee tratteggiate l’andamento delle pressioni in camera positiva ed in camera negativa per il nostro caso di riferimento (0 spessori in camera positiva, 0 spessori in camera negativa, 200 Psi, temperatura 20*C).
Da notare come ovviamente entrambe le curve partono dalla stessa pressione in quanto al 0% di compressione le due camere sono in comunicazione.
Molte volte quando sento parlare di progressività di un ammortizzatore noto che si analizza solamente la variazione di pressione in camera positiva, ma questo è sbagliato poiché le due camere (positiva e negativa) nel bilancio delle pressioni risultanti ovviamente si influenzano a vicenda.
La curva che ci interessa per l’analisi dell’ammortizzatore è quella chiamata “pressione esterna” (poi vedremo perché la chiamo cosi), essa non è altro che la differenza tra le pressioni tra camera positiva e camera negativa nello stesso punto di affondamento.
La pressione esterna relativa ad un dato affondamento non è altro che la pressione applicata dall’esterno all’ammortizzatore per far si che esso si comprima di tale valore di affondamento.
Verifica modello teorico
Se consideriamo il sistema ammo-bici-rider, la pressione agente direttamente sull’ammortizzatore non è altro che il rapporto tra la “Forza peso” del rider agente sul posteriore della bici e l’ ”Area di base del pistone” interno, tutto questo diviso per il “Rapporto di leva del carro”. Essendo l’ “Area di base del pistone” e il “Rapporto di leva del carro” due quantità costanti, capiamo come la “Pressione esterna” sarà direttamente proporzionale al peso del rider e quindi alla sua “Forza peso” (Forza esterna).
Vediamo di calcolare il peso del rider partendo dai dati ricavabili dal grafico in modo da avere la controprova sull’affidabilità del modello teorico da me studiato.
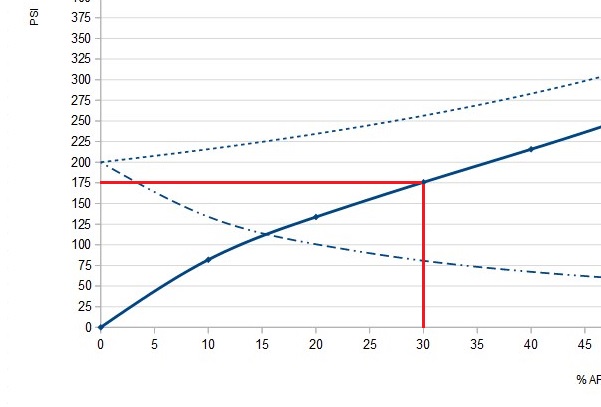
Da FIG. 8 vediamo che la pressione applicata dall’esterno all’ammortizzatore per far si che esso si comprima del 30% è pari a 175 Psi.
Trasformiamo la pressione in Pascal (uniformiamo tutte le grandezze al S.I.), quindi moltiplichiamola per 6894,76 in quanto 1 Psi =6894,76 Pa.
Supponiamo che la distribuzione dei pesi (quella usata per il calcolo empirico del SAG del 30%) sulla bike sia del 35% ant e 65% post.
Calcoliamo il rapporto di leva del carro, semplificando in lineare l’andamento dello stesso, per la bici sulla quale è stato montato l’ammortizzatore in prova (Specialized Enduro 650b) esso è di 165mm (corsa della ruota) / 57mm (corsa dell’ammortizzatore) = 2,9.
A questo punto abbiamo tutti i dati e il peso del rider che verrà calcolato dovrebbe essere di circa 82kg (come nella misurazione empirica della mia bilancia in bagno) per avere la controprova sulla bontà del modello teorico.
P = 175 Psi
A pistone= 0,0013 m2
RL = 2,9
Distribuzione peso al posteriore= 65%
——–P * 6894,76 * A
F = ————————– = P * 4,755 = 832,125 Newton —-> 83,2 kg
————RL * 0,65
Il dato relativo la forza peso ,ricavato dai calcoli è quindi molto vicino al valore reale (82 kg), l’aumento di 1,3 kg può essere ricondotto alla progressività del carro (della quale non abbiamo tenuto conto) oppure ad approssimazioni di calcolo, o agli attriti.
Possiamo concludere che il modello teorico da me elaborato di analisi è VALIDO.
Sappiamo ora anche che le pressioni in Psi sull’asse delle ordinate possono essere ricondotte al peso del rider moltiplicandole semplicemente per 0,4755 (per avere il risultato in kg e non in N).
Analisi delle curve
A questo punto analizziamo la curva delle “Pressione esterna” in FIG. 7.
Vediamo che per far partire la compressione dell’ammortizzatore la forza è un infinitesimo superiore a 0Psi(nella realtà questo non è esattamente verò poiché ci sono sempre degli attriti relativi alle tenute dell’ammortizzatore e nel caso di ammo montato sulla bici anche gli attriti relativi agli snodi del carro) ,
capiamo quindi l’utilità di avere una camera negativa alla stessa pressione di quella positiva con ammo a riposo.
Per arrivare al 30% di compressione abbiamo bisogno di una pressione di 175Psi, tradotta in 83Kg di rider se si fa riferimento al sistema ammo-bici-rider.
Il fondocorsa è a 720Psi (tradotti in 342,3 Kg statici).
Se riusciamo a trasformare una qualsiasi sollecitazione proveniente dall’esterno (come ad esempio l’effetto di un drop da 1m di altezza) in Newton possiamo indagare su quale sarà la compressione dell’ammo (trascurando l’intervento dell’idraulica).
Stuck down
Se avessimo una pressione in camera negativa superiore a quella attesa allora l’ammo si troverebbe in “Stuck down” , ovvero non riuscirebbe a riestendersi completamente in situazione di riposo e parte della corsa sarebbe persa. Questo può accadere se per caso l’ammo viene sgonfiato mentre è compresso o talvolta se la bici rimane capovolta per lungo tempo.
Per rimediare basta riestendere a forza lo stelo in modo da aprire la valvola di comunicazione tra le camere ed equilibrare la pressione oppure gonfiare la camera positiva fino a raggiungere la pressione di quella negativa, oppure nel peggiore dei casi (quasi sempre per quanto mi riguarda) bisogna sfiatare la camera negativa smontando l’ammo.
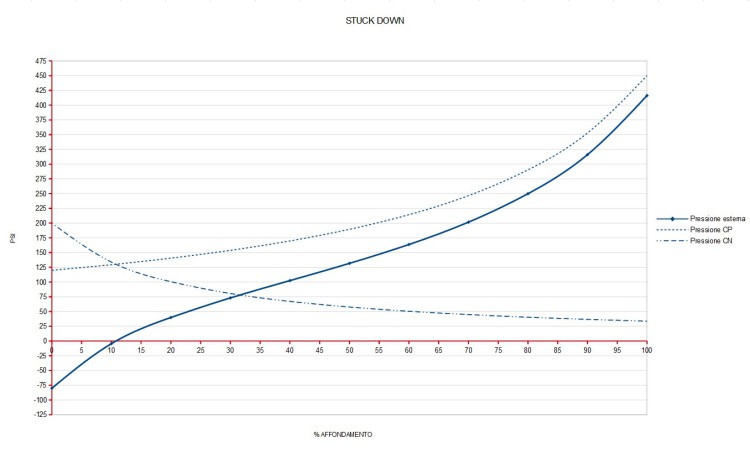
Analizziamo attraverso il grafico di FIG. 9 la situazione di “Stuck down”.
La camera negativa a 0% di affondamento virtuale si trova a pressione superiore di quella positiva (esempio di ammo sfiatato ad ammo compresso), 200Psi in camera negativa e 120Psi in camera positiva. L’equilibrio delle pressioni si troverà nel punto di intersezione delle due curve, attorno al 10% di affondamento nel caso in esempio.
In questa situazione l’ammo non riuscirà a riestendersi mai completamente e perderà il primo 10% di corsa.
Confronto set-up diversi
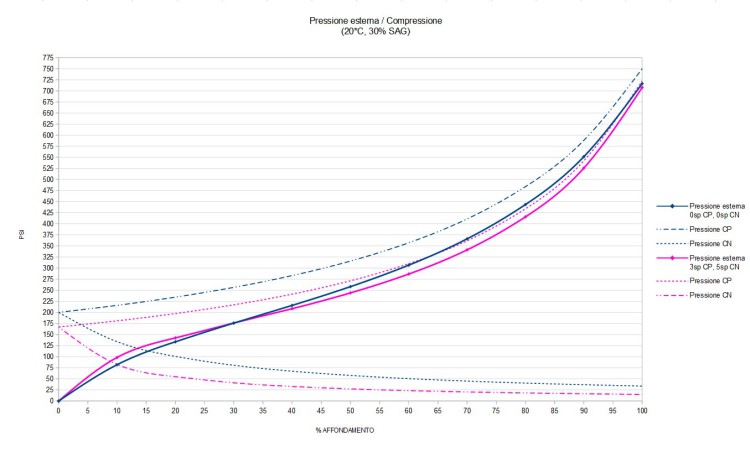
Osserviamo ora il grafico successivo. In FIG. 10, abbiamo due setup diversi, il nostro di riferimento e quello con 0 spessori in camera positiva e ben 5 in camera negativa , ovvero il massimo concesso.
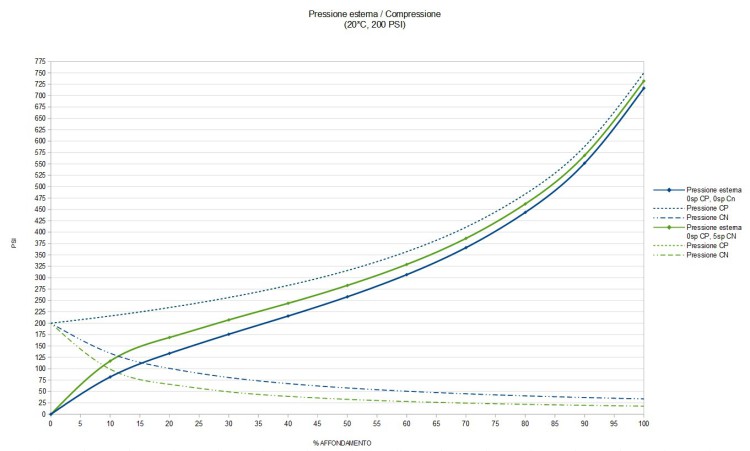
Questo grafico non è particolarmente indicativo poiché notiamo che avendo modificato gli spessori ma avendo mantenuto la stessa pressione iniziale di 200Psi, per l’ammo spessorato il sag del 30% non si attesterà più su 175Psi (83Kg) ma bensi a 205Psi (97 Kg). Con un peso di 83 Kg (175Psi) il sag relativo all’ammo spessorato sarà di circa 22%, e a noi questo non va bene. Dobbiamo quindi sgonfiare l’ammo. Ma di quanto?
Attraverso il mio evolutissimo (..) modello di calcolo ho trovato facilmente la pressione di gonfiaggio, che sarà di 169Psi.
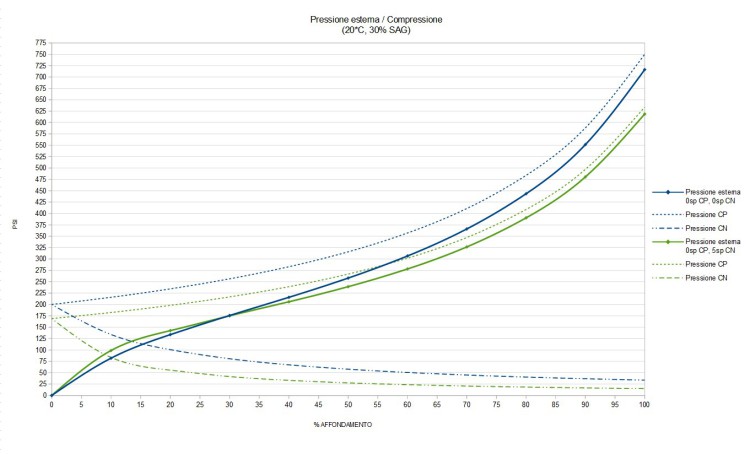
Vediamo nel grafico di FIG. 11 come calando opportunamente la pressione iniziale avremo lo stesso sag del 30% per lo stesso peso di rider (83 Kg).
Possiamo quindi analizzare come influiscono sulla curva della Pressione esterna gli spessori in camera negativa. L’ammo spessorato in negativa presenterà una resistenza maggiore all’affondamento nella prima parte di corsa, tale affermazione è facilmente verificabile misurando il Lavoro (fisicamente parlando) che dovrà fare l’ammo per raggiungere il 30% di affondamento, e per farlo basta calcolare l’area sottesa alla curva.
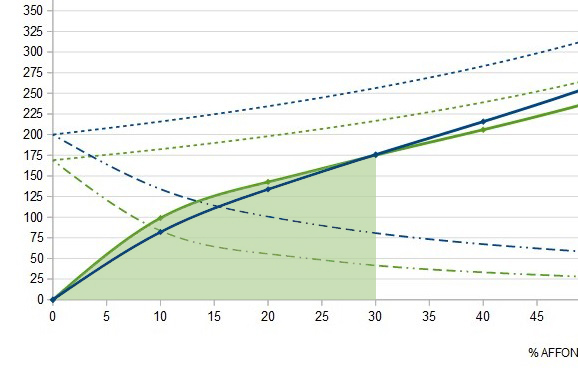
Si vede facilmente che l’area sottesa alla curva verde (FIG. 12) è maggiore a quella sottesa alla curva blu (FIG. 13). Nella pratica ciò si traduce in una minore sensibilità ai piccoli urti nella prima parte di corsa e ad un minor effetto oscillatorio dovuto alle forze relative alla pedalata.
Da FIG. 11 notiamo come dal 30% di affondamento in poi l’ammo spessorato in negativa si farà più sensibile rispetto a quello non spessorato in negativa ma sarà meno progressivo, raggiungerà quindi il fine corsa più facilmente.
Analizziamo ora gli altri casi limite e poi confrontiamoli tutti assieme, sarà facile a questo punto trarre le dovute conclusioni su come le variazioni di vuolume in camera positiva ed in camera negativa influenzano il comportamento dell’ammo.
9 spessori cp , 0 spessori cn
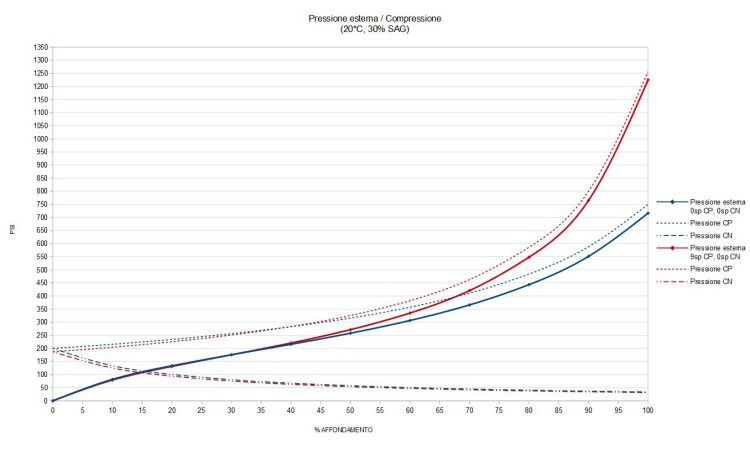
Pressione gonfiaggio = 187 Psi
9 spessori cp, 5 spessori cn
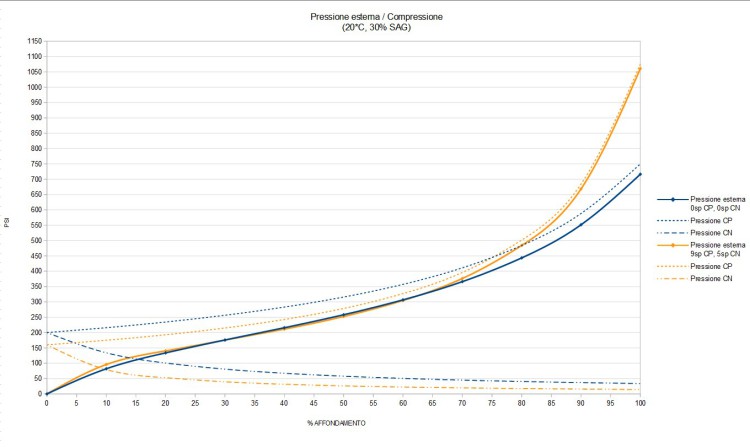
Pressione gonfiaggio = 160 Psi
Confronto globale
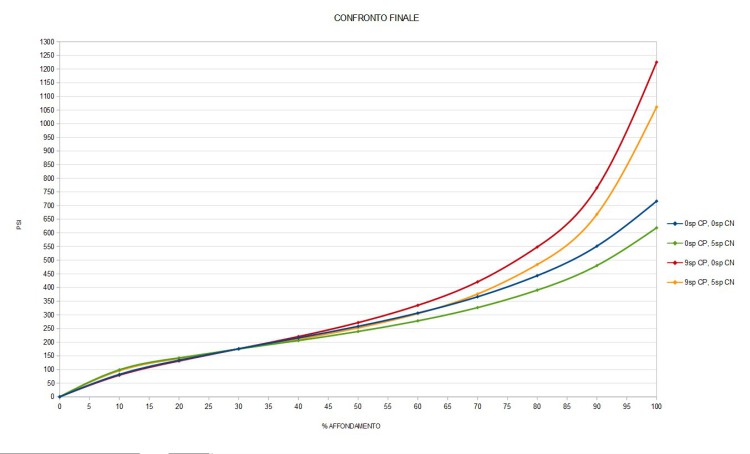
Osservazioni finali
Capiamo quindi che per ottenere un risultato soddisfacente nella modifica dei volumi bisogna farlo con cognizione di causa e non “a caso”. Bisognerà trovare il giusto rapporto tra pressione iniziale, spessori in positiva e spessori in negativa in modo da ottenere il meglio dal nostro ammortizzatore.
Se ad esempio volessimo aumentare la resistenza all’affondamento nella prima parte di corsa ma mantenere circa la medesima progressività nel fine corsa dovremo spessorare certamente la camera negativa, ma anche la positiva, e dovremo cercare la giusta pressione per avere il nostro sag voluto.
Analizziamo l’ esempio nel grafico di FIG.17. Ho voluto aumentare la resistenza all’oscillazione della pedalata mantenendo comunque l’ammo progressivo verso la fine della corsa. Per fare ciò ho spessorato al massimo la camera negativa e successivamente con il mio programma di calcolo mi sono trovato gli spessori necessari da mettere in camera positiva e la pressione di gonfiaggio affinchè la forza necessaria a mandare l’ammortizzatore a fine corsa sia più o meno la medesima
Questo discorso sugli spessori ovviamente è valido per ammo spessorabili ma spiega anche bene la differenza di funzionamento tra ammortizzatori aventi volumi interni diversi tra loro, quindi tra modelli diversi e marche diverse, o tra stesso modello in versione standard e High Volume.
[ad45]











